在计算机科学领域中,我们经常需要进行十六进制和十进制之间的转换。虽然这两种数制表示方式有所不同,但通过一些简单的公式和方法,我们可以轻松地实现它们之间的相互转换。本文将介绍这些转换的公式和方法,并通过实例分析来加深理解。
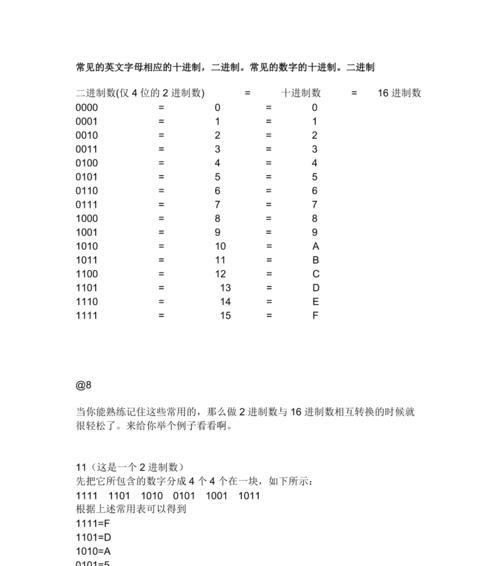
一:十六进制和十进制的基本概念与区别
十六进制是一种基数为16的数制,它使用0-9以及A-F表示10-15这六个额外的数字。而十进制则是我们平时使用的基数为10的数制,其中使用0-9这十个数字。理解这两种数制的基本概念和区别对于转换十分重要。
二:十六进制转换为十进制的公式及步骤
十六进制转换为十进制可以通过将每个十六进制位数乘以对应的权重,再将结果相加来实现。例如,对于十六进制数ABCD,转换为十进制可以使用公式:

(16^3*A)+(16^2*B)+(16^1*C)+(16^0*D)=十进制数。接下来,我们将详细介绍如何进行转换。
三:十进制转换为十六进制的公式及步骤
与十六进制转换为十进制类似,十进制转换为十六进制也可以通过一系列的步骤实现。将十进制数除以16得到商和余数,余数即为转换后的十六进制数的最低位。将商再次除以16,并重复上述步骤,直到商为0为止。按照得到的余数的逆序排列即可得到转换后的十六进制数。
四:十六进制与十进制相互转换的例题分析1
通过一个具体的例题来加深对于十六进制与十进制相互转换的理解。例如,将十六进制数0x2A转换为十进制。我们可以将其拆解为(16^1*2)+(16^0*A),然后将A转换为对应的十进制数10。最终计算结果为(16*2)+10=42。

五:十六进制与十进制相互转换的例题分析2
继续通过例题来巩固转换方法。例如,将十进制数128转换为十六进制。我们可以将其拆解为(16^2*0)+(16^1*8)+(16^0*0),最终计算结果为80。
六:将二进制转换为十六进制或十进制的方法
在计算机领域中,我们常常需要将二进制数转换为十六进制或十进制。这可以通过先将二进制数转换为十进制,再将十进制数转换为目标数制来实现。例如,将二进制数1101转换为十六进制,首先将其转换为十进制得到13,然后将十进制数13转换为十六进制即为D。
七:将十六进制或十进制转换为二进制的方法
同样地,我们也需要将十六进制或十进制数转换为二进制。这可以通过先将十六进制或十进制数转换为十进制,再将十进制数转换为二进制来实现。例如,将十六进制数B转换为二进制,首先将其转换为十进制数11,然后将十进制数11转换为二进制即为1011。
八:十六进制与十进制相互转换的应用举例
十六进制与十进制的相互转换在计算机科学领域中有广泛的应用。例如,在存储器中,十六进制常用于表示内存地址,而十进制常用于表示数据的大小。通过将十六进制地址转换为十进制,我们可以更好地理解数据的存储和访问。
九:十六进制与十进制的相互转换在编程中的重要性
在编程中,我们经常需要进行进制之间的转换。十六进制与十进制之间的转换在处理颜色、文件格式、网络地址等方面非常重要。掌握这些转换方法可以帮助我们更好地理解和处理这些数据。
十:十六进制与十进制相互转换的注意事项
在进行十六进制与十进制相互转换时,需要注意边界情况和输入的合法性。例如,在将十六进制转换为十进制时,需要确保输入的每个位数均合法,并且没有超出范围。否则,转换结果可能会出现错误。
十一:十六进制与十进制转换的实际应用案例
除了计算机科学领域,十六进制与十进制相互转换也在其他领域有实际应用。例如,在金融领域中,十六进制数常用于表示股票代码。通过将股票代码转换为十进制,我们可以更好地理解和分析股市数据。
十二:十六进制与十进制转换的性能分析
虽然十六进制与十进制之间的转换方法相对简单,但在实际应用中,我们仍需考虑其性能。比如,在大规模数据转换时,选择高效的转换算法和工具可以提高计算效率。
十三:十六进制与十进制转换的未来发展趋势
随着计算机科学的不断发展,十六进制与十进制相互转换的方法也在不断改进。未来,我们可以预见出现更多智能化、自动化的工具和算法,使得转换更加便捷和高效。
十四:十六进制与十进制转换的实践与学习建议
要掌握十六进制与十进制之间的相互转换,除了理论知识,还需要进行实际的练习和应用。建议读者多做转换练习题,并结合实际场景进行实践,才能更好地掌握这一技能。
十五:
通过本文的介绍,我们了解了十六进制与十进制之间的相互转换公式和方法,并通过实例分析加深了对其应用的理解。掌握这些转换技巧对于计算机科学和其他领域的学习和应用都具有重要意义。希望读者能够通过学习和实践,更加熟练地应用十六进制与十进制的相互转换。
标签: #网络设备









