在数学中,开平方和开立方是非常常见的计算方法,它们能够帮助我们求得一个数的平方根或立方根。本文将探索开平方和开立方的奥秘,介绍它们的计算方法以及应用。
平方根与立方根的定义与概念
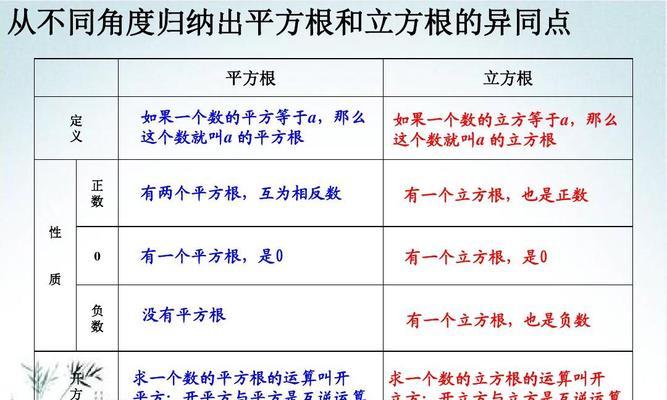
1.平方根的定义:平方根是指一个数的二次方等于该数的正数。
2.立方根的定义:立方根是指一个数的三次方等于该数的正数。
开平方的计算方法与例题
3.直接提取法:当一个数的平方是一个完全平方数时,可以直接提取其平方根。
4.除法逼近法:当一个数的平方不是一个完全平方数时,可以利用除法逼近法来计算其平方根。
开立方的计算方法与例题
5.试探法:通过试探不同的整数来逼近一个数的立方根。
6.牛顿迭代法:利用牛顿迭代法可以更精确地计算一个数的立方根。
开平方和开立方在实际生活中的应用
7.建筑领域中的应用:开平方和开立方可以用于计算建筑物的面积、体积等。
8.金融领域中的应用:开平方和开立方可以用于计算利息、投资回报率等。
9.工程领域中的应用:开平方和开立方可以用于计算电流、功率等。
开平方和开立方的简便计算方法
10.近似计算法:当精确计算开平方和开立方比较困难时,可以使用近似计算法来得到一个估计值。
11.科学计算器的使用:现代科学计算器已经内置了开平方和开立方的计算功能,可以方便地进行相关运算。
开平方和开立方的数学性质与特点
12.二次根与三次根的性质:二次根和三次根具有一些特殊的数学性质,例如它们的范围、符号等。
13.根与幂的运算规律:根与幂之间存在一些运算规律,例如乘法法则、除法法则等。
不同数值的开平方和开立方
14.负数的开平方与开立方:负数的开平方和开立方需要引入虚数单位i来进行计算。
15.小数的开平方与开立方:对小数进行开平方和开立方时,可以利用近似计算法或科学计算器进行求解。
通过本文的介绍,我们了解了开平方和开立方的定义、计算方法及应用。这些方法和技巧在实际生活中有着广泛的应用,帮助我们更准确地进行数值计算。在进一步研究数学的同时,我们也能够更好地理解数学在现实生活中的实际应用。
深入探索平方与立方的奥秘
数学中的平方和立方一直是人们探索的重要内容,它们在各个领域都有着广泛的应用。本文将深入研究开平方和开立方的原理和方法,揭示其中的奥秘,并展示数学的魅力。
段落
1.平方和立方的定义及应用
平方是指一个数与自己相乘,立方是指一个数与自己相乘两次。平方和立方在几何、物理等领域都有着广泛的应用,例如计算面积、体积等。
2.为什么需要开平方和开立方
在实际问题中,我们经常需要求出一个数的平方根或立方根,这就需要用到开平方和开立方的方法。比如求解勾股定理中的斜边长度、计算物体的体积等。
3.开平方的原理和方法
开平方是指求一个数的平方根。通过推导,我们可以得出求一个数的平方根的一般公式。还有牛顿迭代法、二分法等方法可以用来近似求解。
4.开立方的原理和方法
开立方是指求一个数的立方根。与开平方类似,我们可以通过推导得出求立方根的一般公式。同时,牛顿迭代法、二分法等也可以用于近似求解。
5.开平方和开立方的特殊情况
平方根和立方根并不是所有数都能精确求解的,有些数只能通过近似方法求解。特殊情况下,如负数的平方根和立方根,我们需要引入复数的概念。
6.开平方和开立方的计算工具
在现代科技的发展下,我们不再需要手工计算平方根和立方根,而是可以使用计算器或电脑软件进行计算。这大大提高了计算效率。
7.平方与立方在几何中的应用
平方与立方在几何中有着广泛的应用,如计算图形的面积、体积等。通过平方和立方,我们可以更好地理解和描述几何形状。
8.平方与立方在物理中的应用
物理学中经常涉及到平方和立方的运算,如速度的平方、物体的体积等。这些应用帮助我们更好地理解和解决物理学中的问题。
9.平方与立方的数学性质
平方与立方具有一些特殊的数学性质,如平方数的性质、立方数的性质等。研究这些性质可以拓展我们对平方和立方的认识。
10.平方与立方的历史发展
平方和立方作为数学中的重要概念,拥有着悠久的历史。我们可以追溯到古希腊时期,了解平方和立方的起源和发展过程。
11.平方与立方的拓展应用
平方和立方不仅在几何和物理中有应用,还在其他领域中发挥着重要作用,如金融学、计算机科学等。探索这些拓展应用可以深化对平方和立方的认识。
12.平方与立方的挑战
虽然我们已经有了开平方和开立方的方法,但对于一些特殊的数,求解其平方根和立方根仍然是一项挑战。这促使数学家们继续探索更高级的算法。
13.平方与立方的实际问题解析
我们可以通过一些实际问题来解析平方和立方的应用,如求解物体的体积、计算三角形的边长等。这将帮助我们更好地理解和应用平方和立方。
14.平方与立方的奇妙关系
平方与立方之间存在着一种奇妙的关系,通过这种关系,我们可以发现一些有趣的数学规律和性质。深入研究这种关系,会给我们带来意想不到的发现。
15.数学的魔力与平方立方的奥秘
通过深入探索开平方和开立方的原理和方法,我们不仅解锁了数学中的魔力,也揭示了平方和立方背后的奥秘。这让我们更加热爱数学,也更加欣赏数学的美妙。
标签: #怎么