在数学中，直线是一条无限延伸的、只有长度没有宽度的几何对象。而直线方程则是描述直线位置的一个重要工具。本文将围绕两点直线方程公式展开讨论，从推导过程到应用场景，带领读者深入了解这一数学概念的内涵。
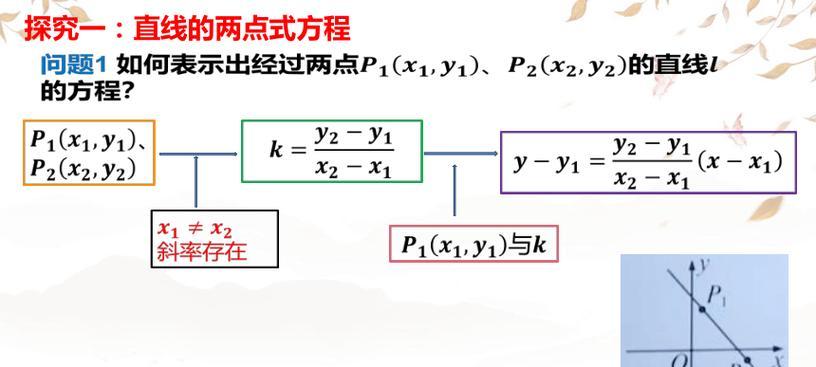
定义与背景
1.直线的基本概念和特性
2.直线方程的作用和重要性
点斜式的推导与应用
3.点斜式的定义和推导过程
4.点斜式在解析几何中的应用场景
5.点斜式在实际问题中的应用案例
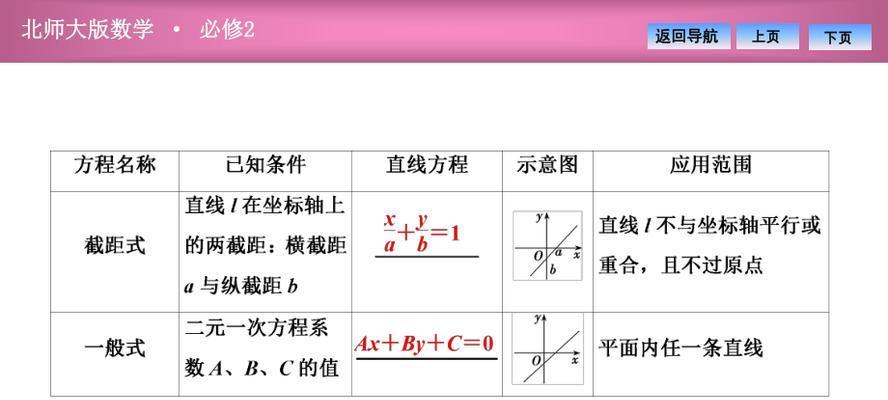
截距式的推导与应用
6.截距式的定义和推导过程
7.截距式在解析几何中的应用场景
8.截距式在实际问题中的应用案例
一般式的推导与应用
9.一般式的定义和推导过程
10.一般式在解析几何中的应用场景
11.一般式在实际问题中的应用案例
两点直线方程公式的比较与选择
12.点斜式、截距式和一般式的特点和适用范围比较
13.如何根据实际情况选择合适的直线方程形式
两点直线方程公式的变形与扩展
14.两点直线方程公式的变形及其推导过程
15.扩展应用：直线方程的三维推导和应用
通过本文的讲述，我们深入了解了两点直线方程公式的推导过程和应用场景。在解析几何中，掌握直线方程的不同形式和相应的推导方法，可以更好地理解和运用直线方程解决实际问题。同时，我们也了解到直线方程的应用并不仅限于二维平面，还可以扩展到三维空间中。希望读者通过这篇文章，对直线方程有更全面的了解，并能在实际问题中灵活应用。
版权声明：
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容， 请发送邮件至 3561739510@qq.com 举报，一经查实，本站将立刻删除。！
标签： #方程公式
